TALLER12: SISTEMA DE ECUACIONES LINEALES

Solución de Sistemas de Ecuaciones Lineales.
El problema fundamental del Álgebra Lineal consiste en la resolución del sistema de ecuaciones

donde u = (ul, . . ., uN) es el vector buscado, f = (fl, f2,..., fN) es un vector conocido de dimensión N, A = (aij) (i, j = 1, 2, . . ., N) es una matriz cuadrada de dimensión NxN con elementos aij.

Se supondrá inicialmente que la matriz A es regular, es decir que su determinante es distinto de cero, de modo que la ecuación Au = 0 tiene sólo una solución trivial, y el sistema (1) tiene la única solución

EJERCICIO

Veamos con un ejemplo concreto cómo resolver un sistema de ecuaciones lineales a través del Excel. En esencia utilizaremos la fórmula (2), es decir, primero calcularemos la matriz inversa y luego multiplicaremos la matriz inversa por el término libre. Este esquema se basa en que en Excel existen dos funciones apropiadas para esto y que comentaremos mas adelante que son MINVERSA, que devuelve la matriz inversa de una matriz y la función MMULT, que devuelve el producto matricial de dos matrices. Estas funciones son ejemplos de las llamadas fórmulas matriciales del ExUna fórmula matricial puede ejecutar varias operaciones y devolver un único resultado o varios resultados. Las fórmulas matriciales actúan en uno, dos o más conjuntos de valores denominados argumentos matriciales. Las fórmulas matriciales se crean del mismo modo que las demás fórmulas, excepto que al concluir su introducción se debe presionar la combinación de teclas CTRL+MAYÚS+ENTRAR.

Cuando se introduce una fórmula matricial, Microsoft Excel inserta de forma automática la fórmula entre llaves ({}).

Supongamos se desea resolver el sistema:

cuya solución es obviamente:

Para ello introduzcamos la matriz del sistema (3) y el vector libre como un bloque rectangular de 5 filas y 6 columnas en una hoja de Excel tal y como se muestra a continuación:

Ahora procederemos a calcular la matriz inversa de la matriz del sistema. Para ello: seleccionaremos un bloque vacío de 5x5 donde se ubicará la matriz inversa y con el rango de 5x5 celdas seleccionado se oprime el signo “=” (significa que se introducirá una fórmula);

Luego mediante el asistente de funciones seleccionamos la función MINVERSA;

Esta fórmula tiene un argumento que es la matriz que se desea invertir. Por ello el Excel nos pide que introduzcamos dicho argumento en el diálogo que se muestra a continuación. Observe que aquí podemos sencillamente introducir el rango de celdas correspondientes a la matriz original u oprimir el botón   que permite seleccionar este rango de celdas mediante el ratón.

Puede apreciarse que escribimos el rango A1:E5 que corresponde a la matriz original del Sistema (3). Una vez establecido el rango se oprime el botón aceptar y se obtiene el siguiente resultado:

Aparentemente, no se ha obtenido la respuesta esperada pues sólo se ha calculado el valor de la primera celda de la matriz inversa. Realmente el problema es que queda un paso importante que es convertir la fórmula a una fórmula matricial. Para ello basta con hacer clic con el ratón en la barra de fórmulas y oprimir CTRL+MAYÚS+ENTRAR. Una vez que se hace esto se obtiene:

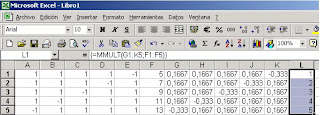
Nótese que la fórmula aparece ahora encerrada entre llaves, lo que indica que es una fórmula matricial. En el rango G1:K5 aparece la matriz inversa a la matriz del sistema y basta con multiplicar esta matriz por el vector libre para obtener la solución del sistema (3). Para ello seleccionemos el rango de celdas donde depositaremos el producto (que debe ser un vector columna), por ejemplo podríamos seleccionar el rango L1:L5 y repitiendo los pasos anteriores mediante el asistente de funciones seleccionamos la función MMULT luego de lo cual aparece un diálogo para que determinemos los argumentos de esta fórmula:

Aquí evidentemente debemos introducir en Matriz1 el rango G1:K5 que es donde se aloja la matriz inversa ya calculada y en Matriz 2 el rango F1:F5 que es donde está almacenado el vector libre del sistema (3). Una vez aceptados los parámetros y convertida la fórmula a matricial obtendremos:

Observe que ya se obtuvo en el rango L1:L5 la solución correcta (4).

Si no existe seguridad de que la matriz del sistema sea no degenerada es conveniente chequear esta condición primero. Para ello el Excel soporta la función MDETERM que calcula el determinante de una Matriz. Si el determinante es distinto de cero, podemos proseguir con el proceso descrito anteriormente, si es igual cero se necesitarían otros métodos para calcular las soluciones (si existen) del sistema. La función MDETERM no es una función matricial.